Monday, 1 April 2013
Monday, 18 March 2013
Trial papers!
Hi! So these are SPM trial papers (Mod Mathematics) in three different states;
Perak (2012)
Paper 1: http://www.scribd.com/doc/104858774/Trial-Mathematics-Spm-Perak-2012-Paper-1
Paper 2: http://www.scribd.com/doc/104858835/Trial-Mathematics-Spm-Perak-2012-Paper-2
Answer: http://pelajaranperak.gov.my/v2/modules/mastop_publish/files/files_5046ac3c63443.zip
Melaka (2012)
Paper 1: http://www.4shared.com/office/ZszcQq1S/Matematik_K1_SPM_Melaka_2012.html
Paper 2: http://www.mediafire.com/?f7fbcw65lgcg4cb
Pahang (2012)
Paper 1: http://www.mediafire.com/?722vge8x9gyj3se
Paper 2: http://www.mediafire.com/?sb3xu3scmwwmmue
Answer: http://www.scribd.com/doc/105712164/Trial-Mathematics-Spm-Pahang-2012-Answer
All the best :)
-Iman Ridhuan-
Perak (2012)
Paper 1: http://www.scribd.com/doc/104858774/Trial-Mathematics-Spm-Perak-2012-Paper-1
Paper 2: http://www.scribd.com/doc/104858835/Trial-Mathematics-Spm-Perak-2012-Paper-2
Answer: http://pelajaranperak.gov.my/v2/modules/mastop_publish/files/files_5046ac3c63443.zip
Melaka (2012)
Paper 1: http://www.4shared.com/office/ZszcQq1S/Matematik_K1_SPM_Melaka_2012.html
Paper 2: http://www.mediafire.com/?f7fbcw65lgcg4cb
Pahang (2012)
Paper 1: http://www.mediafire.com/?722vge8x9gyj3se
Paper 2: http://www.mediafire.com/?sb3xu3scmwwmmue
Answer: http://www.scribd.com/doc/105712164/Trial-Mathematics-Spm-Pahang-2012-Answer
All the best :)
-Iman Ridhuan-
Sunday, 17 March 2013
Saturday, 16 March 2013
Friday, 15 March 2013
HISTORY OF MATH
The area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, to a less extent, an investigation into the mathematical methods and notation of the past.
Before the modern age and the worldwide spread of knowledge, written examples of new mathematical developments have come to light only in a few locales. The most ancient mathematical texts available are Plimpton 322 (Babylonian mathematics c. 1900 BC), the Rhind Mathematical Papyrus (Egyptian mathematics c. 2000-1800 BC)and the Moscow Mathematical Papyrus (Egyptian mathematics c. 1890 BC). All of these texts concern the so-called Pythagorean theorem, which seems to be the most ancient and widespread mathematical development after basic arithmetic and geometry.
The study of mathematics as a subject in its own right begins in the 6th century BC with the Pythagoreans, who coined the term "mathematics" from the ancient Greek μάθημα (mathema), meaning "subject of instruction".Greek mathematics greatly refined the methods (especially through the introduction of deductive reasoning and mathematical rigor in proofs) and expanded the subject matter of mathematics.Chinese mathematics made early contributions, including a place value system.The Hindu-Arabic numeral system and the rules for the use of its operations, in use throughout the world today, likely evolved over the course of the first millennium AD in India and was transmitted to the west via Islamic mathematics.Islamic mathematics, in turn, developed and expanded the mathematics known to these civilizations.Many Greek and Arabic texts on mathematics were then translated into Latin, which led to further development of mathematics in medieval Europe.
From ancient times through the Middle Ages, bursts of mathematical creativity were often followed by centuries of stagnation. Beginning in Renaissance Italy in the 16th century, new mathematical developments, interacting with new scientific discoveries, were made at an increasing pace that continues through the present day.
Games Time
Check out this really fascinating game! It is called Multiplication game.
The aim of the game is to get 4 in a row faster than the computer. It is like the game Othello.
All you have to do is, move the markers on the number line to make products and try to line 4 products in a row. You can only move one marker to form the product while the other marker has to stay stationary.
Enjoy and good luck!
Click Multiplication Game to try this game out.
-Cheryl Chin-
The aim of the game is to get 4 in a row faster than the computer. It is like the game Othello.
All you have to do is, move the markers on the number line to make products and try to line 4 products in a row. You can only move one marker to form the product while the other marker has to stay stationary.
Enjoy and good luck!
Click Multiplication Game to try this game out.
-Cheryl Chin-
Tuesday, 26 February 2013
Get these Angles Grammar right
| Acute Angle | an angle that is less than 90° |
| Right Angle | an angle that is 90° exactly |
| Obtuse Angle | an angle that is greater than 90° but less than 180° |
TONGUE TWISTER II
Denise sees the fleece
Denise sees the fleece,
Denise sees the fleas.
At least Denise could sneeze
and feed and freeze the fleas.
Felt
Of all the felt I ever felt I never felt felt that felt like that felt felt.
How much wood would a woodchuck chuck
How much wood would a woodchuck chuck if a woodchuck could chuck wood?
How much wood would a woodchuck chuck if a woodchuck could chuck wood?
How much wood would a woodchuck chuck if a woodchuck could chuck wood in a truck?
As much wood as a woodchuck could if a woodchuck could chuck wood?
I slit the Sheet
I slit the sheet,
The sheet I slit
and on the slitted sheet I sit.
Peter Piper
Peter Piper picked a peck of pickled peppers.
A peck of pickled peppers Peter Piper picked.
If Peter Piper picked a peck of pickled peppers,
Where's the peck of pickled peppers Peter Piper picked?
TONGUE TWISTER
A Canner Can
A canner exceedingly canny
one morning remarked to his granny
"a canner can can
anything that he can
but a canner can't can a can, can he?"
(Carolyn Wells)
A Tutor
A tutor who tooted the flute
Tried to tutor two tooters to toot
Said the two to the tutor
"Is it tougher to toot Or to tutor two tooters to toot?"
Beebee and Phoebe
A certain young fellow named Beebee
Wished to marry a lady named Phoebe
"But," he said. "I must see What the minister's fee be
Before Phoebe be Phoebe Beebee
A canner exceedingly canny
one morning remarked to his granny
"a canner can can
anything that he can
but a canner can't can a can, can he?"
(Carolyn Wells)
A Tutor
A tutor who tooted the flute
Tried to tutor two tooters to toot
Said the two to the tutor
"Is it tougher to toot Or to tutor two tooters to toot?"
Beebee and Phoebe
A certain young fellow named Beebee
Wished to marry a lady named Phoebe
"But," he said. "I must see What the minister's fee be
Before Phoebe be Phoebe Beebee
RIDDLES
Three Guys at A Hotel Riddle
Three guys rent a hotel room for the night. When they get to the hotel they pay the $30 fee, then go up to their room. Soon the bellhop brings up their bags and gives the lawyers back $5 because the hotel was having a special discount that weekend. So the three lawyers decide to each keep one of the $5 dollars and to give the bellhop a $2 tip. However, when they sat down to tally up their expenses for the weekend the could not explain the following details:Each one of them had originally paid $10 (towards the initial $30), then each got back $1 which meant that they each paid $9. Then they gave the bellhop a $2 tip. HOWEVER, 3 • $9 + $2 = $29The guys couldn't figure out what happened to the other dollar. After all, the three paid out $30 but could only account for $29.
Can you determine what happened?
There are many ways of explaining/thinking about this truly brain bending riddle! It all boils down to the fact that the lawyers's math is incorrect. They did NOT spend $9 • 3 + $2.
They spent exactly $27 dollars. $25 for the room and $2 for the tip. Remember they got exactly $3, in total back.
Every farmer's part is 1/3(45+75) = 40 sacks.
Charlie paid $1400 for 40 sacks, then 1 sack costs $1400/40 = $35/sack.
Adam got $35*(45-40)=35*5 = $175.
Ben got $35*(75-40)=35*35 = $1225.
Answer: Ben $1225, Adam $175
They spent exactly $27 dollars. $25 for the room and $2 for the tip. Remember they got exactly $3, in total back.
Another way to think about the answer to this riddle is to just pretend that the bellhop refunded $3 to the lawyers (rather than giving them $5 and receiving $2 back). If the lawyers get $3 back and each takes $1. They they spent exactly $27 dollars.
Three Brothers on a Farm
Three brothers live in a farm. They agreed to buy new seeds: Adam and Ben would go and Charlie stayed to protect fields. Ben bought 75 sacks of wheat in the market whereas Adam bought 45 sacks. At home, they split the sacks equally. Charlie had paid 1400 dollars for the wheat. How much dollars did Ben and Adam get of the sum, considering equal split of the sacks?Every farmer's part is 1/3(45+75) = 40 sacks.
Charlie paid $1400 for 40 sacks, then 1 sack costs $1400/40 = $35/sack.
Adam got $35*(45-40)=35*5 = $175.
Ben got $35*(75-40)=35*35 = $1225.
Answer: Ben $1225, Adam $175
MATH JOKES
If you had 8 apples in one hand and 5 apples in the other, what would you have?
(Really big hands!)
What is a mathematician's favorite dessert?
(Pi!)
How can you make seven even?
(Take away the "s"!)
What has eight legs and eight eyes?
(Eight pirates!)
SETS
Definition
What is a set? Well, simply put, it's a collection.
First you specify a common property among "things" (this word will be defined later) and then you gather up all the "things" that have this common property.
For example, the items you wear: these would include shoes, socks, hat, shirt, pants, and so on.
I'm sure you could come up with at least a hundred.
This is known as a set.
|
Or another example would be types of fingers.
This set would include index, middle, ring, and pinky.
|
So it is just things grouped together with a certain property in common.
Notation
There is a fairly simple notation for sets. You simply list each element, separated by a comma, and then put some curly brackets around the whole thing.
The curly brackets { } are sometimes called "set brackets" or "braces".
This is the notation for the two previous examples:
{socks, shoes, watches, shirts, ...}
{index, middle, ring, pinky}
{index, middle, ring, pinky}
Monday, 25 February 2013
Average formula:
Let a1,a2,a3,......,an be a set of numbers, average = (a1 + a2 + a3,+......+ an)/n
Fractions formulas:
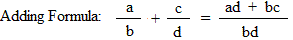
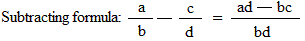
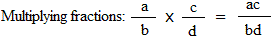
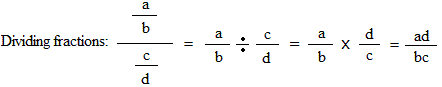
Converting a mixed number to an improper fraction:
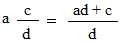
Converting an improper fraction to a mixed number:

Formula for a proportion:
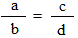
In a proportion, the product of the extremes (ad) equal the product of the means(bc),
Thus, ad = bc
Percent:
Percent to fraction: x% = x/100
Percentage formula: Rate/100 = Percentage/base
Rate: The percent.
Base: The amount you are taking the percent of.
Percentage: The answer obtained by multiplying the base by the rate
Consumer math formulas:
Discount = list price × discount rate
Sale price = list price − discount
Discount rate = discount ÷ list price
Sales tax = price of item × tax rate
Interest = principal × rate of interest × time
Tips = cost of meals × tip rate
Commission = cost of service × commission rate
Geometry formulas:
Perimeter:
Perimeter of a square: s + s + s + s
s:length of one side
Perimeter of a rectangle: l + w + l + w
l: length
w: width
Perimeter of a triangle: a + b + c
a, b, and c: lengths of the 3 sides
Area:
Area of a square: s × s
s: length of one side
Area of a rectangle: l × w
l: length
w: width
Area of a triangle: (b × h)/2
b: length of base
h: length of height
Area of a trapezoid: (b1 + b2) × h/2
b1 and b2: parallel sides or the bases
h: length of height
volume:
Volume of a cube: s × s × s
s: length of one side
Volume of a box: l × w × h
l: length
w: width
h: height
Volume of a sphere: (4/3) × pi × r3
pi: 3.14
r: radius of sphere
Volume of a triangular prism: area of triangle × Height = (1/2 base × height) × Height
base: length of the base of the triangle
height: height of the triangle
Height: height of the triangular prism
Volume of a cylinder:pi × r2 × Height
pi: 3.14
r: radius of the circle of the base
Height: height of the cylinder
Let a1,a2,a3,......,an be a set of numbers, average = (a1 + a2 + a3,+......+ an)/n
Fractions formulas:
Converting a mixed number to an improper fraction:
Converting an improper fraction to a mixed number:
Formula for a proportion:
In a proportion, the product of the extremes (ad) equal the product of the means(bc),
Thus, ad = bc
Percent:
Percent to fraction: x% = x/100
Percentage formula: Rate/100 = Percentage/base
Rate: The percent.
Base: The amount you are taking the percent of.
Percentage: The answer obtained by multiplying the base by the rate
Consumer math formulas:
Discount = list price × discount rate
Sale price = list price − discount
Discount rate = discount ÷ list price
Sales tax = price of item × tax rate
Interest = principal × rate of interest × time
Tips = cost of meals × tip rate
Commission = cost of service × commission rate
Geometry formulas:
Perimeter:
Perimeter of a square: s + s + s + s
s:length of one side
Perimeter of a rectangle: l + w + l + w
l: length
w: width
Perimeter of a triangle: a + b + c
a, b, and c: lengths of the 3 sides
Area:
Area of a square: s × s
s: length of one side
Area of a rectangle: l × w
l: length
w: width
Area of a triangle: (b × h)/2
b: length of base
h: length of height
Area of a trapezoid: (b1 + b2) × h/2
b1 and b2: parallel sides or the bases
h: length of height
volume:
Volume of a cube: s × s × s
s: length of one side
Volume of a box: l × w × h
l: length
w: width
h: height
Volume of a sphere: (4/3) × pi × r3
pi: 3.14
r: radius of sphere
Volume of a triangular prism: area of triangle × Height = (1/2 base × height) × Height
base: length of the base of the triangle
height: height of the triangle
Height: height of the triangular prism
Volume of a cylinder:pi × r2 × Height
pi: 3.14
r: radius of the circle of the base
Height: height of the cylinder
MATH SHAPE FORMULA
| Shapes |
Formula
|
| Rectangle: Area = Length X Width A = lw Perimeter = 2 X Lengths + 2 X Widths P = 2l + 2w | |
| Parallelogram Area = Base X Height a = bh | |
| TriangleArea = 1/2 of the base X the height a = 1/2 bh Perimeter = a + b + c (add the length of the three sides) |
| Trapezoid Perimeter = area + b1 + b2 + c P = a + b1 + b2 + c | |
| Circle Try the Online tool. The distance around the circle is a circumference. The distance across the circle is the diameter (d). The radius (r) is the distance from the center to a point on the circle. (Pi = 3.14) More about circles. d = 2r c = pd = 2 pr A = pr2 (p=3.14) | |
| Rectangular Solid Volume = Length X Width X Height V = lwh Surface = 2lw + 2lh + 2wh | |
| Prisms Volume = Base X Height v=bh Surface = 2b + Ph (b is the area of the base P is the perimeter of the base) | |
| Cylinder Volume = pr2 x height V = pr2 h Surface = 2p radius x height S = 2prh + 2pr2 | |
| Pyramid V = 1/3 bh b is the area of the base Surface Area: Add the area of the base to the sum of the areas of all of the triangular faces. The areas of the triangular faces will have different formulas for different shaped bases. | |
| ConesVolume = 1/3 pr2 x heightV= 1/3 pr2h Surface = pr2 + prsS = pr2 + prs =pr2 + pr | |
| SphereVolume = 4/3 pr3V = 4/3 pr3 Surface = 4pr2S = 4pr2 |
BASIC MATH SYMBOLS
| Symbol | Symbol Name | Meaning / definition | Example |
|---|---|---|---|
| = | equals sign | equality | 5 = 2+3 |
| ≠ | not equal sign | inequality | 5 ≠ 4 |
| > | strict inequality | greater than | 5 > 4 |
| < | strict inequality | less than | 4 < 5 |
| ≥ | inequality | greater than or equal to | 5 ≥ 4 |
| ≤ | inequality | less than or equal to | 4 ≤ 5 |
| ( ) | parentheses | calculate expression inside first | 2 × (3+5) = 16 |
| [ ] | brackets | calculate expression inside first | [(1+2)*(1+5)] = 18 |
| + | plus sign | addition | 1 + 1 = 2 |
| − | minus sign | subtraction | 2 − 1 = 1 |
| ± | plus - minus | both plus and minus operations | 3 ± 5 = 8 and -2 |
| ∓ | minus - plus | both minus and plus operations | 3 ∓ 5 = -2 and 8 |
| * | asterisk | multiplication | 2 * 3 = 6 |
| × | times sign | multiplication | 2 × 3 = 6 |
| ∙ | multiplication dot | multiplication | 2 ∙ 3 = 6 |
| ÷ | division sign / obelus | division | 6 ÷ 2 = 3 |
| / | division slash | division | 6 / 2 = 3 |
| – | horizontal line | division / fraction | |
| mod | modulo | remainder calculation | 7 mod 2 = 1 |
| . | period | decimal point, decimal separator | 2.56 = 2+56/100 |
| a b | power | exponent | 23 = 8 |
| a^b | caret | exponent |
2 ^ 3 = 8
|
| √a | square root |
√a · √a = a
| √9 = ±3 |
| 3√a | cube root | 3√8 = 2 | |
| 4√a | forth root | 4√16 = ±2 | |
| n√a | n-th root (radical) | for n=3, n√8 = 2 | |
| % | percent | 1% = 1/100 | 10% × 30 = 3 |
| ‰ | per-mille | 1‰ = 1/1000 = 0.1% | 10‰ × 30 = 0.3 |
| ppm | per-million | 1ppm = 1/1000000 | 10ppm × 30 = 0.0003 |
| ppb | per-billion | 1ppb = 1/1000000000 | 10ppb × 30 = 3×10-7 |
| ppt | per-trillion | 1ppb = 10-12 | 10ppb × 30 = 3×10-10 |
Sunday, 3 February 2013
MATH FACTS
- The word 'mathematics' comes from the Greek máthēma, which means learning, study, science.
- What comes after a million, billion and trillion? A quadrillion, quintillion, sextillion, septillion, octillion, nonillion, decillion and undecillion.
- Different names for the number 0 include zero, nought, naught, nil, zilch and zip.
- Zero ( 0 ) is the only number which can not be represented by Roman numerals.
- The name 'zero' derives from the Arabic word sifr which also gave us the English word 'cipher' meaning 'a secret way of writing' .
- Do you know the magic of no. nine (9)? Multiply any number with nine (9 ) and then sum all individual digits of the result (product) to make it single digit, the sum of all these individual digits would always be nine (9).
- Here is an interesting trick to check divisibility of any number by number 3.A number is divisible by three if the sum of its digits is divisible by three (3).
- The = sign ("equals sign") was invented by 16th Century Welsh mathematician Robert Recorde, who was fed up with writing "is equal to" in his equations.
MATH JOKES
Halloween
Q: What do you get if you divide the circumference of a jack-o-lantern by its diameter?
A: Pumpkin Pi
A: Pumpkin Pi
Mathematicians at the beach
Q: Why do you rarely find mathematicians spending time at the beach?A: Because they have sine and cosine to get a tan and don't need the sun
Zero said to eight
Q: What does the zero say to the the eight?A: Nice belt!
Fear
Q. Why is the number six scared of seven?A. Because seven eight nine (7 ate 9)!
Subscribe to:
Posts (Atom)







